卷积神经网络 – 图像处理常见的方法
这篇文章我们介绍机器学习中的卷积神经网络(Convolutional Neural Networks, CNN),卷积神经网络是深度学习的代表算法之一。卷积神经网络(CNN)在很多领域都有非常广泛的应用,最常见的是用于处理图像数据。
1、卷积神经网络的典型应用方式
卷积神经网络(CNN)是基于神经网络技术(参见什么是神经网络)的一种发展,也是根据输入数据,得到预测结果。例如,将一幅图像输入CNN模型,判断出该图像上是否是猫,甚至判断猫是什么品种。
卷积神经网络在图像领域的输入和输出
卷积神经网络(CNN)的输入:图像-具体指的是图像中的像素矩阵
- 简单的情况可以用一个二维矩阵代表一张黑白图片,矩阵中的每个值表示对应像素的灰度。
- 更典型的方式是可以用三维矩阵代表一张图片,其中,三维矩阵的长和宽代表了图像的大小,而三维矩阵的深度代表了图像的色彩通道。比如黑白图片的深度为1,而在RGB色彩模式下,图像的深度为3。例如,一张300分辨率的一寸RGB照片,即该照片的像素为295*413,此时输入的三维矩阵就是(295,413,3)。可以理解为这是3个二维矩阵,分别对应RGB(红绿蓝)一种颜色的深度。每个二维矩阵就称为一个通道。
卷积神经网络(CNN)的典型输出:对图片的预测结果。
- 例如,预测的结果是图片中是猫,更进一步图片中的是一只缅因猫。
- 这个结果可以是二分类结果、多分类结果,也可以是单个值或多个值的预测结果。
以上仅为CNN图像识别功能示例,CNN还可以用于其他方面。而且CNN还可以与其他模型结构进行组合,实现更强大的功能。
2、卷积神经网络的结构
实际上,CNN可以理解为C+NN,其中C是指卷积(Convolution),NN是指神经网络,其本质上就是在普通的神经网络的基础上添加了卷积和池化操作。需要注意的是,这里的NN大部分时候采用的是全连接神经网络,关于全连接神经网络的介绍,这里不赘述,详情可参照文章——全连接神经网络的介绍。
图1展示的是一个典型的CNN结构。对于输入矩阵,先对通过一层卷积层做卷积处理,提取出特征矩阵,然后通过一层池化层,对特征矩阵进行压缩处理,最后输入到全连接神经网络中,在图3中对应的是全连接层和输出层组成的全连接神经网络。值得注意是,CNN可以根据目标选择多个卷积层和池化层对输入特征进行提取压缩,而每一次的卷积和池化可以使用不同的策略。
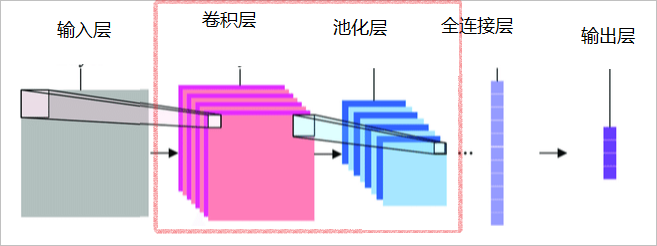
根据图1我们亦可以看到,粉色方框中圈出的部分就是CNN在一般的全连接神经网络的基础上添加的内容。因此就不难理解,CNN最后的输出,可以和神经网络的输出是类似的。
一个重点要理解的是,CNN输出的这个抽象特征,与神经网络的隐藏层输出的结果是比较类似的,都是代表了之前输入数据的一些内在性质,但没有显性的、可解释的含义。
但要注意,这里只是粗浅的介绍。实际上,这里说的卷积处理还包括了很多细节,而模型的结构也可以有各种发展变化,CNN必须要包含至少一层卷积层即可。
3、什么是卷积
对于像图像、文字这种信息量多、信息含量复杂的数据,这类数据原始输入特征矩阵会非常庞大,所以对其做分类等处理的时候必须要对特征矩阵进行浓缩处理。而卷积处理就是对高信息量的特征矩阵进行浓缩处理的关键。
卷积层是CNN 中最为重要的部分。卷积处理是用一个卷积核对一个图像块做处理,得到一个处理后的值,这个值代表了被处理的图像块的特征。也有时将卷积核称为滤波器。
卷积核本质上是一个权重矩阵,卷积处理实际上是个函数运算,这个运算的具体方法在这里不细说。有兴趣的可以参见卷积神经网络。
如图2所示,图中左边数字1部分是原始输入数据,在本例子中为输入像素矩阵,图中中间数字2部分是卷积核(滤波器filter),图中右边数字3部分是输出的新的二维数据,该数据则是代表该像素矩阵区域的新的特征值。图中右上角数字4部分展示了从数字1到数字3部分的计算过程。
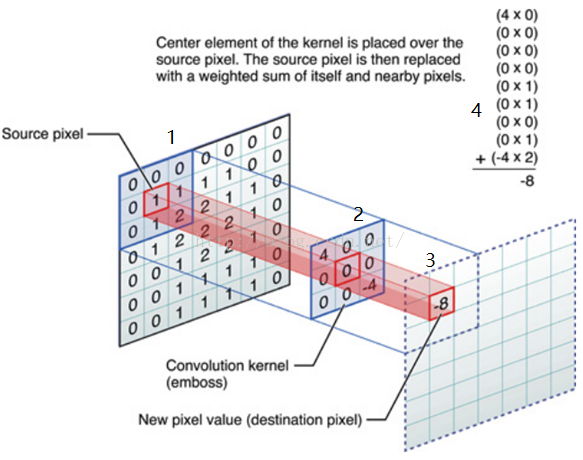
在图3中我们只展示了对输入图像的像素矩阵中的某一部分进行卷积,实际上在整个处理过程中,我们将会对像素矩阵进行遍历操作,从而完成对整个图像的卷积操作。操作时还会针对边缘情况做些处理,相关的细节也不在这里赘述了,有兴趣可以可以参照文章——卷积对边缘点的处理。
简单来讲,卷积处理就是对输入特征矩阵的每一部分作用一个卷积核得到新的特征矩阵的过程。通过图像处理的例子通俗来讲就是,在原始图片上确定一个像素窗口大小,遍历图片的每一块像素窗口,通过自定义的策略将这窗口内的像素值进行函数映射从而形成新的像素值的过程,新形成的像素矩阵(也就是新图片)的大小会根据策略的不同而变化。卷积处理本质上是对特征的浓缩,是一种降维和特征抽取的过程。卷积后的数据受临近像素的相互的影响,即该卷积后的数据不仅是反映出本身的一个像素的信息,而且可以将相邻像素的信息共同反映出来。而具体受到邻近多少像素点的影像是由卷积窗口(像素窗口)和卷积核决定的。
那么,一个自然的问题就是,卷积核是怎么确定的呢?
答案是:卷积核是训练出来的。它是模型参数的一部分。
4、CNN的训练
概括地讲,CNN的训练与其他有监督学习模型的训练方法是一样的,都是基于样本数据和标签进行训练。可以参见机器学习基本概念中的训练部分。
例如,可以将大量图片作为训练样本,将是猫的图片标为1,不是猫的图片标为0,就可以训练出一个判断图片是否为猫的CNN模型。
CNN训练所更新模型的参数,除了神经网络中的参数外,还至少包括卷积核。
5、CNN中的一些典型变化
实际应用中的CNN,还包括很多细节和变化。在此只做一些粗浅的介绍。
- 池化层:
池化一般接在卷积过程后。池化,也叫Pooling,其本质其实就是是采样。池化对于输入的图片,选择某种方式对其进行压缩,以加快神经网络的运算速度。这里说的某种方式,其实就是池化的算法, 比如最大池化(Maxpooling)或平均池化(Averagepooling)。在卷积神经网络中通常会在相邻的卷积 层之间加入一个池化层,池化层可以有效的缩小参数矩阵的尺寸, 从而减少最后连接层的中的参数数量。所以加入池化层可以加快计算速度和防止过拟合的作用。
图3将展示一个使用maxpooling的池化层过程:
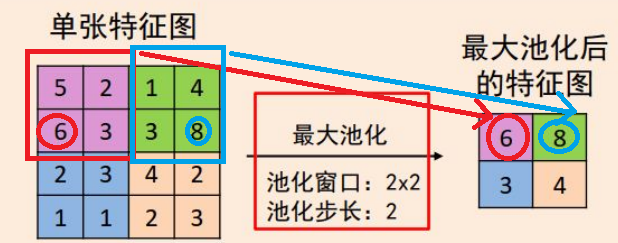
图3左边的矩阵描述的是输入特征矩阵,蓝色方框与蓝色箭头对应的是一次池化过程、蓝色圆圈对应的是该次池化结果,右侧矩阵对应的是整个特征矩阵的池化结果,即输出的特征矩阵。值得注意的是,图中的红色框(或蓝色框)称为池化窗口,而池化窗口滑动的距离就是池化步长,在图3中就是红框到蓝框的滑动距离。同样的,在池化过程中也将会对输入的整个特征矩阵进行遍历,从而提取出新的特征矩阵。
- 激活函数
激活函数就是运行在神经元上,负责改造输入到输出的映射,使得其可以无限逼近任意非线性函数映射。在不使用激活函数的神经网络中,也就是最原始的感知机(感知机详情参见文章——最全面的感知机总结),只是对输入进行加权求和,得到输出。通过感知机得到的输入与输入时线性组合的关系,无法满足非线性的情况。激活函数的主要作用就是给模型增加非线性感知能力,使得神经网络的输入和输出之间不只是线性组合关系,使得模型在非线性的情况下有良好的结果。一般常使用的激活函数有sigmod函数和softmax函数,具体可参照文章——常用激活函数总结进行了解。
- 多层卷积
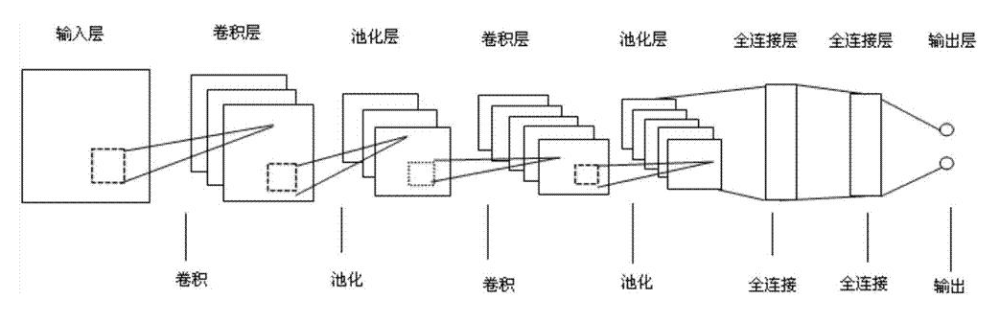
在实际过程中,只含有一层卷积的CNN很难满足应用,故而通常情况下会根据目标计划多层卷积,如图4所示。值得注意的是每一层卷积层的后面通常会接一层池化层对卷积结果进行压缩,池化层的池化窗口池化步长的选择通常要依据目标进行调整。一般来说,卷积层和池化层的布局通常是倒推的,也就是根据结果和输入的规模选择卷积和池化的规模;卷积核和卷积窗口、步长的选取每一层可以不同,池化亦然。
举例来说,如果输入矩阵大小为128*128、输出矩阵大小为13*1(在分类中也就是分为13类),那么只有一层的情况下,卷积层的大小为m*n,池化层的大小n*13(m、n为任意正整数),多层情况下以此类推。

