向量距离与聚类
一、向量距离
在机器学习中通常用向量来表示每个样本,因此向量和样本之间存在一一对应的关系。
那么样本之间的差异可以用向量的相似度衡量,而向量之间的相似度,可以通过计算向量之间的距离来衡量。
样本之间的向量距离越近,样本之间相似度较高,样本之间越相似。

如上图所示,P1、P2、P3为三个不同数据在坐标系中的坐标点位,可以清楚看到,P1和P2两点之间的直接距离明显小于P1和P3两点之间的直接距离。此处的直接距离体现在向量空间中即为向量距离,即P1和P2的向量距离小于P1和P3的向量距离。
根据前述相似度与向量距离之间的关系,我们可以得出,P1和P2之间的相似度大于P1和P3之间的相似度。
向量距离的计算方式
计算向量距离有多种方法,例如欧式距离、余弦距离、马氏距离、切比雪夫距离、曼哈顿距离等。其中,欧式距离最为简单,即前述P1、P2、P3三个点坐标的直接距离。
下面我们可以再简单介绍一下余弦距离:
把两个向量看成空间中的两条线段,都是从原点([0, 0, …])出发,指向不同的方向。两个向量出发点相同,但方向不同,自然就形成了夹角。而余弦相似度就是利用夹角余弦值来衡量。
余弦值的范围在[-1,1]之间:
值越趋近于1,代表两个向量的夹角越接近0度,因此向量方向越接近,相似度越高;
值越趋近于-1,代表两个向量的夹角越接近180度,因此向量方向越相反,相似度越低;
值接近于0,代表两个向量的夹角越接近90度,表示两个向量近乎于正交,我们称之为两者独立。
如上图所示,A,B是三维空间中的两个向量,其中dist(A,B)为A,B间的欧氏距离,这两个点与三维空间原点连线形成角θ,即为A,B间的余弦距离。
如果角度θ越小,说明这两个向量在方向上越接近,相似度也更高,因此在聚类可以归成一类。
余弦距离的具体计算方式与其他向量距离的计算方法此处不再赘述,可以参见《向量空间中各类距离表示》。
二、聚类
聚类和分类的区别
说到聚类,应先理解聚类和分类的区别,两者经常被混为一谈,但其实二者之间有本质的区别。
说的通俗易懂一点,这两种操作都会把数据进行划分,但方法有所不同,两者最简单的区别就是类别是否已知。
分类(Classification)注重的是数据本身的特征及类别,需要用类别做标签进行划分,因此需要事先知道类别信息,从而将不同数据划为不同类别;
聚类(Clustering)不需要类别做标签,不需要事先知道类别信息,只需要计算数据之间相似程度,将相似度高的划为一类。
因此,分类是一种监督学习(Supervised Learning)方法,聚类是一种无监督学习(Unsupervised Learning)方法。
举例:
- 分类:在日常使用谷歌邮箱Gmail的过程中,可以人工对于每一封邮件点选“垃圾”或“不是垃圾”,过一段时间,Gmail就可以自动过滤掉一些垃圾邮件。这是因为在点选的过程中,其实是给每一条邮件打了一个“标签”,这个标签只有两个值:垃圾”或“不是垃圾”,Gmail就会不断研究哪些特点的邮件是垃圾,哪些特点的邮件不是垃圾,形成一些判别的模式,这里可以视作一个简单的机器学习的过程。长此以往,当一封信的邮件到来,Gmail就可以自动把邮件分到“垃圾”和“不是垃圾”这两个我们人工设定的分类的其中一个。
- 聚类:有一大堆的邮件,设定好的算法会对这部分邮件的数据进行建模分析,基于数据之间的向量距离等来判断数据之间的相似性,从而对这部分邮件数据进行聚类,得到划分成不同类的邮件。与依据标签的分类过程不同,在聚类结果得出之前,我们往往不知道邮件会被分成几类、每一类有什么特点,需要根据聚类结果结合人的经验来分析得出结论。聚类之后,我们可能会得到“垃圾”和“不是垃圾”的聚类结果,也可能得到“工作邮件”、“私人邮件”和“广告邮件”的聚类结果等。
定义
聚类是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。也即将相似度高的数据尽可能聚集到一起,相似度低的数据尽量分离。
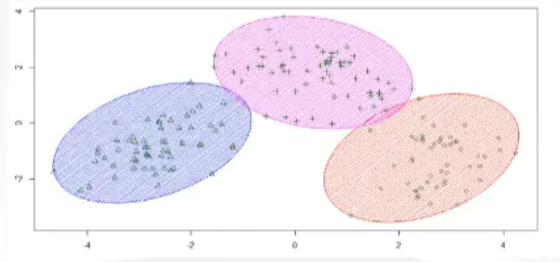
如上图所示,可以将数据进行聚类,不同颜色表示不同的类。
聚类算法
参见的聚类算法有K-Means(K均值)聚类、均值漂移聚类、基于密度的聚类方法(DBSCAN)、用高斯混合模型(GMM)的最大期望(EM)聚类、凝聚层次聚类、图团体检测(Graph Community Detection)等,此处不进行详述,相关资料可参考:《常见的六大聚类算法》。
聚类中心
聚类中心,可以理解为一个聚类的代表,是指聚类分析中可以用来代表该类别的一个特殊样本。其他样本通过计算与聚类中心的向量距离来决定是否属于该类(近的属于,远的不属于)。
聚类中心可以是一个存在的具体样本,也可以是一个计算出来的样本,实际并不存在。
因为其他样本通过计算与聚类中心的向量距离来决定是否属于该类,所以聚类中心是需要在聚类分析之前提前选择。
示例
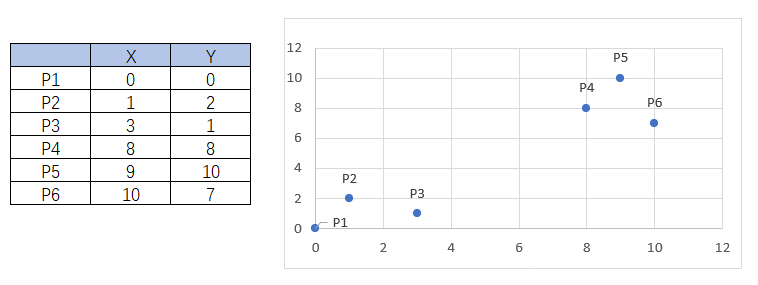
两种聚类中心的选择方式:
①可以选择P2、P4为聚类中心(也可以选择其他的点),根据勾股定理可计算出其余各个点分别到P2、P4的距离,通过距离比较,确定聚类结果是:类1:P1、P2、P3 类2:P4、P5、P6
②可以选择两个虚拟的点Pn(1.33,1) 和Pm(9,8.33)(提前计算出来的),根据勾股定理可计算出其余各个点分别到Pn、Pm的距离,通过距离比较,确定聚类结果是:类1:P1、P2、P3 类2:P4、P5、P6
每个聚类算法有其对应的确定聚类中心和判断聚类完成的方式,此处不再详述。
三、向量距离与聚类的联系
我们是基于样本之间的向量距离对样本进行聚类的,向量距离是进行样本聚类的数值依据。简单来说,可以将向量距离较近的样本聚为一类。这就是两者之间的联系。

