正则化

正则化（Regularization）

正则化，是在机器学习模型训练时采用的一种方法，其作用就是降低模型的复杂度，从而减少过拟合。

降低模型的复杂度，粗略地理解，就是使模型的参数（比如做矩阵计算时，矩阵中非零的单元）少一些。

实际上，也可以把接近于零的元素认为是零。

正则化的方法，具体地讲，就是在训练模型时，在损失函数中加一个正则化项。这个正则化项反映的是模型中参数的复杂度。

我们知道，训练的过程是调整参数，使损失函数尽量变小。在原始的损失函数中，包括的损失项，反映的是预测值与标签值的差异，训练的目的是使预测值与标签值更接近。

而加入正则化项后，训练时使损失函数尽量变小，就同时有两个目的了。一个是之前说的，使预测值与标签值更接近。另一个是使正则化项也要尽量小，也就是使参数别太复杂。

我们基于一个具体的损失函数公式来进一步理解一下上面的内容：

假设存在一个机器学习模型存在参数θ_j，其不加正则项的损失函数为C₀，则加入正则项后，损失函数变为：

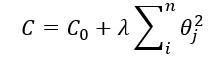
我们希望损失函数C最小，当λ很大时，θ_j就会变小，甚至趋近于0。参数θ_j越小，那么模型中参数θ_j对应的特征对模型影响也将变小甚至没有，模型越不容易过拟合。

简单地理解就是，通过加入一个正则项，在最小化新的损失函数的时候，正则项使得预测值与真实值之间的误差并不会达到最小，也就是说它是不会去完美拟合的，这样也就防止了过拟合，提高了机器学习模型的泛化能力。